Зміст
- Значення та основне застосування
- Види та форми
- Методи швидкого отримання результату
- Невизначені інтеграли
- Формули для вирішення
- Основні правила обчислення
- Методи складання
- Рішення»по частинах"
- Навіщо потрібна інтеграція по частинах?
- Складність деяких рівнянь
- Визначений інтеграл як межа суми
- Укладення
Диференціювання та інтегрування - це рівняння, що містить похідні. Останні, якщо дотримуватися математичним властивостям, поділяються на звичайні і приватні. Похідні представляють швидкість зміни, а диференціальне рівняння описує взаємозв`язок між величиною, яка постійно модифікується в процесі розв`язання, утворюючи нові змінні.
Професор університету з легкістю зорієнтується в складних операціях з інтегралами, перетворює їх в одне ціле, а потім доведе обчислення зворотним методом. Однак можливість швидко згадувати деталі складних формул доступна не кожній людині, тому рекомендується освіжити пам`ять або відкрити для себе новий матеріал.
Значення та основне застосування
У науковій літературі похідна визначається, як швидкість, схильна до перетворення функції на основі однієї з її змінних. Диференціація-це сутність обчислення, яку можна порівняти з початком пошуків дотичної до точки. Як відомо, остання має різні види і вимагає обчислювальних формул для пошуку. Припустимо, вам потрібно знайти нахил дотичної до графіка в точці Р. Як це зробити? Досить провести дугоподібну смугу через позначений об`єкт і підняти її вгору, поки ми не отримаємо посічену лінію.

Функція f в х називається диференційованою в точці х = а, якщо похідна f `(а) існує на кожному позначенні її області. Продемонструємо приклад:
f `(а) = lim (h=0) × F (А + h) – f (а) / h
Для того щоб рівняння піддати диференціювання і інтегрування функцій так, що її розташування стане можливим в будь-якій точці x, вона не повинна перериватися. Заздалегідь побудувавши схематичне зображення ви зможете переконатися в достовірності твердження. Саме з цієї причини область f `(х) визначається існуванням її меж.
Припустимо, що Р = f (х) – функція з х, то похідна від f (х) задається як dy / dx. Також вона визначається, як лінійне рівняння, де необхідно знайти необхідні дані по у.
Однак, якщо ми шукаємо похідну від у в першому випадку, то в наступному належить знайти f (x) від x.
d/dx × (f(x)) la або df / DX la
Отже, позначення швидкості зміни функції f (x) щодо x в точці a, що лежить на її поверхні.
Якщо відома похідна f`, яка є диференційованою у своїй області, то ми можемо знайти її значення f. В інтегральному обчисленні ми називаємо F антипохідною або примітивною функцією f `. Метод його розрахунку відомий, як антидиференціювання або інтеграція.
Види та форми
Рівняння з одним або декількома членами, яке включає похідні залежної змінної по незалежній, відомо, як диференціал. Інакше кажучи, він складається з безлічі числових значень, звичайних або приватних, що піддаються змінам в процесі вирішення.

На даний момент існують наступні типи диференціальних рівнянь.
Звичайний. Проста рівність, безпосередньо залежна від змінної:
dy/dx + 5x = 5y
З приватними похідними:
dy/dx + dy/dt = x3-t3
d2y/dx2 – c2 × d2y/dt2
Старшого коефіцієнта. Даному виду характерно участь в порядку диференціального рівняння, як продемонстровано на прикладі нижче, де він дорівнює 3. Число вважається найвищим з присутніх:
d3y/dx2 + 5 × dy/dx + y = √x
Функції можуть мати кілька видів, однак, кращим є використання одинарної лапки з характерними формулами інтегрування і диференціювання.
y’ = dy/dx
y’’ = d2y/dx2
y’’’ = d3y/dx3
Лінійний. Змінна, що фігурує в рівнянні, зводиться в ступінь одиниці. Графік такого виду функцій зазвичай є прямою лінією. Наприклад, (3x + 5), але (x3 + 4x2) не відноситься до даного типу, оскільки вимагає іншого рішення.
dy/dx + xy = 5x
Нелінійний. Будь-яке інтегрування і диференціювання рядів з подвійними способами отримання рівності-відносяться до розглянутого виду:
d2y/dx2- ln y = 10
Методи швидкого отримання результату
Недостатньо розглянути форму, щоб розібратися як впоратися і застосувати на практиці отримані знання. В даний час існує кілька способів вирішення диференціальне рівняння.

Це:
- Поділ змінної. Виконується, коли приклад можна зобразити як dy / dx = f (y) g (x). Особливість полягає в тому, що f і g-функції, що належать до своїх значень. Завдяки цьому, завдання слід перетворити: 1 / f (y) dy = g (x) dx. І тільки після перейти до наступного пункту.
- Метод інтегруючого фактора. Використовується, коли приклад має вигляд dy / dx + р. (x) y = q(x), де р. і q є функціями лише x.
Диференціальний обчислення першого порядку виглядають, як y`+ Р (х) y = Q (x), оскільки вони містять необхідні функції і похідну від y. Подальше збільшення в найменуванні діє за тим же принципом. Наприклад, похідні від невідомої функції, можуть виявитися як приватними, так і звичайними.
Невизначені інтеграли
Якщо вам надана швидкість вашого велосипеда, коли ви вирушили на прогулянку, в залежності від часу-чи зможете ви розрахувати пройдену відстань, використовуючи дані про витрачені хвилини? Дане завдання виглядає непосильною ношею, проте інтеграли допоможуть впоратися з цими властивостями максимально ефективно, отримавши результат.
Наукова література акцентує увагу на тому, що вони є зворотною стороною диференціювання. Дійсно, інтеграція-це метод складання речей. Він з`єднує частинки між собою, створюючи щось нове-ціле. Головне в будь-якому схожому прикладі: знайти невизначені інтеграли і перевірити результати інтегрування диференціюванням. Це допоможе уникнути зайвих помилок.
Якщо ви збираєтеся шукати площу будь-якої випадкової кривої, наприклад, y=f (x), то скористайтеся розглянутим методом. Пам`ятайте, що тільки уважність врятує вас від помилки.
Формули для вирішення
Так, познайомившись з основною концепцією диференціювання та інтегрування-зворотного обчислення через функції, необхідно коротко розглянути деякі основи. Вони наведені нижче.

Основні правила обчислення
Такі інтегровані функції, як f (x) легко перевести в рівність, якщо уявити рівняння, як: ∫ f(x) dx = F(x) + C.
Тут F (x) називається анти-похідною або примітивною. f (x) - інтегральна функція. dx-виступає, як додатковий числовий агент. З-інтегрована або довільна постійна. x-виступає в залежності від сторони рівності.
З наведеного вище твердження, можна зробити висновок, що інтегрування і диференціювання рядів-два протилежних один від одного процесу. Разом вони виступають, як одна з видів операцій, спрямована на отримання підсумкового результату, виконуваного над самим рівнянням.
Тепер, коли ми більше знаємо про особливості обчислення, рекомендується виділити переважні відмінності, необхідні для подальшого розуміння:
- Диференціювання та інтегрування здатні одночасно задовольняти правилам лінійності.
- Операції спрямовані на пошук максимально точного рішення, однак, припускають обмеження для їх визначення.
- При диференціюванні поліноміального прикладу результат на 1 менше, ніж ступінь функції, тоді як в разі інтегрування отриманий результат перетворюється в інший, діючи за протилежною схемою.
- Два види рішення, як говорилося раніше, є протилежними один одному. Вони обчислюються за формулами інтегрування та диференціювання.
- Похідна будь-якої функції унікальна, але, з іншого боку, два інтеграли, в одному прикладі, можуть відрізнятися на константу. Саме це правило представляє головну складність під час виконання завдань.
- Маючи справу з похідними, ми можемо розглядати похідні в точці. Майже як і в інтегралах вони надають функції по інтервалу.
- Геометрично похідна описує швидкість зміни величини відносно іншої, тоді як невизначений інтеграл представляє криву. Вона распложена в паралельному напрямку, а також має дотичні під час перетину нерівних ліній з іншими, ортогональними до осі, що представляє змінну.
Методи складання
Якщо ви зіткнулися з проблемою, як застосовується підсумовування для математичних операцій диференціювання інтегрування, слід ретельно ознайомитися з основними формулами. Вони є аксіомою в навчанні, тому використовуються повсюдно. Зверніть увагу, під час застосування на власних прикладах, формули вірні, тільки якщо починаються з i = 1.

Рішення»по частинах"
Часом функція вимагає нестандартного підходу, щоб дістатися до кінцевого результату і задовольнити умовам рівності. Почленное інтегрування і диференціювання рядів засноване на ідентичності, яка виражається: ∫ f(x) g’(x) dx = f (x) g(x) - ∫ f’(x) g(x) dx
Алгоритм розглянутої методики, виглядає наступним чином:
- Висловити інтегровану функцію як добуток двох виразів. Позначимо одне з них f (x), інше g `(x).
- Тепер приступити до виявлення двох інших формул, які можливо застосувати при виконанні першого пункту. Ряд зміниться. Диференціюванням перетворимо f `(x), щоб отримати вирази f (x). Приступаємо до іншої частини-g (x) інтегрується в g`(x). При цьому, dx залишається в початковій формі і не використовується.
- Вставте отримані вирази в формулу по частинах. На цьому процедура закінчується, і тепер ви можете спробувати оцінити новий Інтеграл праворуч, оскільки він став значно простішим для розуміння.
Раніше дані метод задіяв інтегрування по частинах за допомогою матриці. Спосіб увінчався успіхом, але займав багато часу, тому в даний час він застосовується рідше, в особливих випадках, коли рішення практично неможливо знайти. Для цього достатньо помістити f і g `в перший рядок і обчислити f` і g в другій.
Навіщо потрібна інтеграція по частинах?
Ситуації трапляються різні. Часом рішення виявляються куди складніше, ніж на перший погляд. Тому слід виділити основні проблеми, нерідко зустрічаються при почленном інтегруванні і диференціюванні статечних рядів. Розглянемо два основних правила.
По-перше, частина, яку ми маємо намір інтегрувати, тобто вибрана для g `(x), ми повинні мати можливість конвертувати. Зробивши це важливо максимально швидко. Справа в тому, що складне інтегрування для g рідко призводить до поліпшеного інтегралу, підвищуючи складність. Все це негативно позначається на свободі наших дій під час рішень, а також залежить від ступенів, синусів і косинусів. Нехай пошук правильної відповіді займе час, але призведе до правильного, ніж заплутаного.
По-друге, все інше, тобто частина, яку ми маємо намір диференціювати і позначимо F, повинна помітно виділитися після перетворення. Після нескладної процедури ми зауважимо, що новий Інтеграл виявиться більш спрощеним, ніж попередник.

Так, коли ми об`єднуємо два правила і використовуємо його при вирішенні, то отримуємо можливість скористатися диференціюванням і інтегруванням статечних функцій, які має сенс розглядати по частинах.
Існує і спосіб видалення x, що дозволяє ефективно задіяти перетворення в різних ситуаціях. Наприклад, ми можемо легко інтегрувати, помноживши функцію на поліном, який ми скорочуємо за допомогою диференціації.
∫ x2 sin(3x) dx
∫ x7 cos(x) dx
∫x4 e4x dx
Як f ми беремо ступінь x (в більш загальному випадку-многочлен), а також використовуємо g`. Очевидно, що кожне диференціювання зменшує ступінь числа на одиницю, тому, якщо в прикладі вона досить висока-застосуєте почленное інтегрування кілька разів. Це допоможе скоротити час.
Складність деяких рівнянь
В даному випадку мова йде про диференціювання та інтегрування степеневих рядів. Функцію можна розглядати так, ніби x - є областю інтервалу збіжності точок. Правда метод підійде далеко не всім. Справа в тому, що будь-які функції можуть бути виражені у вигляді статечних рядів, перетворюючись в лінійну структуру і навпаки.
Наприклад, дано ex. Ми може виразити його як рівняння, яке насправді є просто нескінченним поліномом. Степеневий ряд легко помітити, обчисливши, але він не завжди ефективний.
Визначений інтеграл як межа суми
Подивіться на наступне графічне інтегрування та диференціювання.

Для того щоб легко розуміти складну функцію, досить ретельно розібратися в ній. Оцінимо область PRSQP між кривою у = f (x), віссю х і координатами "x = а" і " x = b». Тепер розділіть інтервал [A, b] На` n ` рівних підінтервалів, позначених наступним чином: [x0 , x1 ], [x1 , x2 ], [x2 , x3 ]…. [xn - 1 , xn ].
Де x0 = a, x1 = a + h, x2 = a + 2h, x3 = a + 3h… .. xr = a + rh і xn = b = a + nh або n = (b-a) / h. (1). Відзначимо, що при n → ∞ h → 0.
Розглянутий простір PRSQP є сумою всіх» n " підобластей, де кожна визначена на певній посередності [хr-1 , хr ], r = 1, 2, 3… n. При правильному підході, дані функції можна піддати диференціювання та інтегрування для швидкого вирішення.
Тепер подивіться на ABDM на малюнку. На його основі доцільно зробити наступне спостереження про площі: (ABLC) < (ABDCA) < (ABDM).
Також відзначимо, що при h → 0 або хr - хr-1 → 0 всі три області стають практично рівними один одному. Отже, ми маємо:
sn = h [f(x0) + f(x1) + f(x2) + …. f(xn – 1)] = h r=0∑n–1 f(xr) (2)
або Sn = h [f(x1) + f(x2) + f(x3) + …. f(xn)] = h r=1∑n f(xr) (3)
В даному випадку sn і Sn позначають суму площ всіх нижніх і верхніх прямокутників, піднятих над інтервалами [хr–1, хr] для r = 1, 2, 3,..., n відповідно. Щоб поставити це в перспективу, рівняння (1) можна переписати як:
sn< Площа області (PRSQP) < Sn … (4)
Крім того, передбачається, що граничні значення (2) і (3) однакові в обох випадках, і загальним є лише площа під кривою. У підсумку ми маємо:
limn → ∞ Sn = limn → ∞ sn = області PRSQP = ∫ab f(x) dx … (5)
Площа також є граничним значенням простору, яке знаходиться між прямокутниками нижче кривої і над кривою. Для зручності слід звернути увагу на висотку фігури, рівну кривій на лівому краю кожного подинтервала. Отже, рівняння переписується в кінцевий варіант:
∫ab f(x) dx = limn → ∞ h [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
або ∫ab f(x) dx = (b – a) limn → ∞ (1/n) [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
Укладення
Диференціювання та інтегрування відрізняється між собою рядом властивостей, формул і протилежними змінами. Одне не може перетворитися на інше без допомоги. Якщо диференціація допомагає знайти похідну, то інтеграція виконує зовсім іншу дію. Вона додає деякі частини, здатна допомогти зі ступенями, скорочуючи їх або вдосконалити приклад, спростивши.
Також вона застосовується для перевірки диференційованих рівнянь. Інакше кажучи - вони діють, як єдине ціле, що не можуть співіснувати окремо, оскільки доповнюють один одного. Застосовуючи правила, знаючи безліч методик, тепер ви гарантовано вирішите складні завдання.
 Угоди в цивільному праві: поняття, види, форми, порядок укладення
Угоди в цивільному праві: поняття, види, форми, порядок укладення Споживчий попит-це... Визначення поняття, сутність, форми і види
Споживчий попит-це... Визначення поняття, сутність, форми і види Зовнішньоторговельний баланс-це... Визначення поняття, його структура і сутність
Зовнішньоторговельний баланс-це... Визначення поняття, його структура і сутність Жовчна людина-це... Визначення поняття, якості особистості
Жовчна людина-це... Визначення поняття, якості особистості Функціональна стилістика: поняття і визначення
Функціональна стилістика: поняття і визначення Орієнтація на результат: поняття, визначення, основні показники і методика
Орієнтація на результат: поняття, визначення, основні показники і методика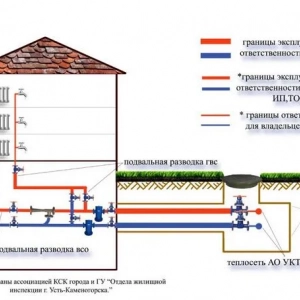 Межа експлуатаційної відповідальності: поняття, юридичне визначення, форми документів нормативні акти, статті, коментарі та відповіді на питання
Межа експлуатаційної відповідальності: поняття, юридичне визначення, форми документів нормативні акти, статті, коментарі та відповіді на питання Мирне співіснування-це... Поняття, визначення, проведення зовнішньої і внутрішньої політики держави
Мирне співіснування-це... Поняття, визначення, проведення зовнішньої і внутрішньої політики держави Комерціалізація інновацій: визначення, поняття, особливості та методи проведення
Комерціалізація інновацій: визначення, поняття, особливості та методи проведення