Зміст
Геометрія є одним з важливих розділів математики. У ньому вивчаються просторові властивості фігур. Однією з них є багатогранник під назвою призма. Дана стаття присвячена відповідям на питання, Що таке призма і які формули застосовуються для розрахунку її основних властивостей.
Многогранник - призма
Почнемо статтю відразу з відповіді на питання, Що таке призма. Під нею розуміють об`ємний багатогранник, який складається з двох багатокутних і паралельних один одному підстав і декількох паралелограмів або прямокутників. Щоб краще уявити, про який клас фігур піде мова, нижче показаний приклад призми п`ятикутної.

Як видно, два п`ятикутника лежать в паралельних площинах і рівні між собою. Їх сторони з`єднані п`ятьма прямокутниками, в даному випадку. З цього прикладу випливає, що якщо підставою фігури є багатокутник з числом сторін n, то кількість вершин призми дорівнюватиме 2 * n, число її граней складе n + 2, а число ребер дорівнюватиме 3 * n. Неважко показати, що кількість цих елементів задовольняє теорему Ейлера:
3 * n = 2 * n + n + 2 - 2.
Вище, коли давалася відповідь на питання, Що таке призма, ми згадали, що грані, що з`єднують однакові підстави, можуть бути паралелограмами або прямокутниками. Зауважимо, що другі відносяться до класу перших. Крім того, можливий випадок, коли ці грані будуть являти собою квадрати. Сторони, які з`єднують основи призми, називаються бічними. Їх кількість визначається числом кутів або сторін багатогранного підстави.
Коротко згадаємо, що значення слова "призма" походить з грецької мови, де це означало буквально "відпиляний". Нескладно зрозуміти, звідки така назва походить, якщо подивитися на чотирикутні дерев`яні призми на малюнку нижче.

Які бувають призми?
Класифікація призм передбачає розгляд різних характеристик цих фігур. Так, в першу чергу враховують багатокутність підстави, тому говорять про трикутних, чотирикутних і інших призмах. По-друге, форма бічних граней визначає, чи є фігура прямою, або ж вона буде похилою. У прямій фігури все бічні грані мають по чотири прямих кута, тобто це або прямокутники, або квадрати. У похилій же фігури ці грані являють собою паралелограми.
До особливої категорії відносяться правильні призми. Справа в тому, що у них підстави являють собою рівносторонні і рівнокутні багатокутники, а сама фігура є прямою. Ці два факти говорять про те, що бічні сторони у таких фігур всі рівні між собою.

Нарешті, ще одним критерієм класифікації є опуклість або увігнутість основи. Наприклад, увігнута фігура у вигляді п`ятикутної зірки показана вище на малюнку.
Формули площі і обсягу правильної фігури
Розібравшись, що таке правильна призма, наведемо дві головні формули, за допомогою яких можна визначити їх обсяг і площа поверхні.
Оскільки площа S всієї фігури утворена з двох підстав з n сторонами і n прямокутниками, то для її обчислення слід користуватися такими виразами:
So = n / 4 * ctg(pi / n) * a2;
S = 2 * So + n * a * h.
Тут So - одного підстави площа, a-сторона цього підстави, h-висота всієї фігури.
Для обчислення обсягу розглянутого виду призм слід застосовувати формулу:
V = So * h = n / 4 * ctg(pi / n) * a2 * h.
Обчислення величин S і V для правильних фігур вимагає знання лише двох лінійних геометричних параметрів.
Трикутна скляна призма
Що таке призма, ми розібралися. Це досконалий об`єкт геометрії, застосовують його для додання форм багатьом спорудам і предметам. Відзначимо лише одне з важливих застосувань її форми у фізиці. Йдеться про трикутної призми, виготовленої зі скла. Завдяки її формі, падаючий на неї світло, в результаті дисперсії розкладається на кілька кольорів, що дозволяє аналізувати хімічний склад випромінювача.
 Геометрична фігура призма. Властивості, види, формули обсягу і площі. Правильна трикутна призма
Геометрична фігура призма. Властивості, види, формули обсягу і площі. Правильна трикутна призма Що таке пряма призма? Формули довжин діагоналей, площі поверхні і обсягу фігури
Що таке пряма призма? Формули довжин діагоналей, площі поверхні і обсягу фігури Що це-пряма призма? Властивості та формули. Приклад завдання
Що це-пряма призма? Властивості та формули. Приклад завдання Що таке нормування: поняття, визначення, види, методи і формули для розрахунків
Що таке нормування: поняття, визначення, види, методи і формули для розрахунків Що таке шлях у фізиці і як його позначають? Формули і приклад задачі
Що таке шлях у фізиці і як його позначають? Формули і приклад задачі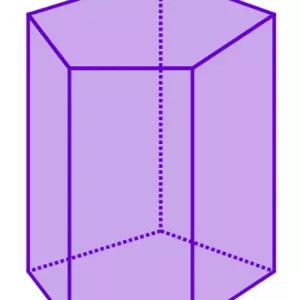 Площа поверхні прямої призми: формули і приклад задачі
Площа поверхні прямої призми: формули і приклад задачі Що таке молярна маса? Молярна маса в хімії та фізиці газів
Що таке молярна маса? Молярна маса в хімії та фізиці газів Масаж шиацу-це що таке? Види і техніка масажу шиацу для омолодження і довголіття
Масаж шиацу-це що таке? Види і техніка масажу шиацу для омолодження і довголіття Енергія кундаліні-що це таке? Кундаліні для активації життєвої енергії
Енергія кундаліні-що це таке? Кундаліні для активації життєвої енергії