Зміст
Вивченням характеристик тривимірних геометричних фігур займається стереометрія. Однією з відомих об`ємних фігур, яка з`являється в задачах геометрії , є пряма призма. Розглянемо в даній статті, що вона собою являє, а також детально охарактеризуємо призму з трикутним підставою.
Призма і її види
Під призмою мають на увазі таку фігуру, яка утворюється в результаті паралельного перенесення багатокутника в просторі. В результаті цієї геометричної операції утворюється фігура, що складається з декількох паралелограмів і двох однакових паралельних один одному багатокутників. Паралелограми є бічними сторонами призми, а багатокутники - це її основи.
Будь-яка призма має n + 2 сторони, 3 * n ребер і 2 * n вершин, де n-число кутів або сторін багатокутної основи. На зображенні показана п`ятикутна призма, яка складається з 7 сторін, 10 вершин і 15 ребер.

Розглянутий клас фігур представлений призмами декількох видів. Перерахуємо їх коротко:
- увігнуті і опуклі;
- похилі і прямі;
- неправильні і правильні.
Кожна фігура відноситься до одного з перерахованих трьох видів класифікації. Під час вирішення геометричних задач найпростіше виконувати розрахунки для правильних і прямих призм. Останні детальніше розглянемо в наступних пунктах статті.
Що це-призма пряма?
Прямий називається увігнута або опукла, правильна чи неправильна призма, у якій всі бічні сторони представлені чотирикутниками з кутами 90°. Якщо хоча б один з чотирикутників бічних сторін не буде прямокутником або квадратом, то призма називається похилою. Можна також дати інше визначення: пряма призма-це така фігура даного класу, у якій будь-яке бічне ребро дорівнює висоті. Під висотою h призми вважають дистанцію між її підставами.
Обидва наведених визначення того, що це-пряма призма, є рівноправними і самодостатніми. З них випливає, що всі двогранні кути між будь-яким з підстав і кожної бічною стороною рівні 90°.
Вище було сказано, що з прямими фігурами зручно працювати при вирішенні завдань. Це пов`язано з тим, що висота збігається з довжиною бічного ребра. Останній факт полегшує процес обчислення обсягу фігури і площі її бічній поверхні.

Обсяг прямої призми
Обсяг-властива будь-якої просторової фігури величина, яка чисельно відображає частину простору, укладеного між поверхнями розглянутого об`єкта. Обсяг призми може бути розрахований за наступною загальною формулою:
V = So*h.
Тобто твір висоти на площу підстави дасть шукане значення V. Оскільки у прямої призми підстави рівні, то для визначення площі So можна брати будь-яке з них.
Перевага використання наведеної вище формули саме для прямої призми в порівнянні з іншими її видами полягає в тому, що висоту фігури знайти дуже просто, так як вона збігається з довжиною бічного ребра.
Площа бічної поверхні
Зручно розраховувати не тільки обсяг для прямої фігури розглянутого класу, але також її бічну поверхню. Дійсно, будь-яка її бічна сторона - це або прямокутник, або квадрат. Як обчислити площу цих плоских фігур, знає кожен школяр, для цього необхідно помножити суміжні сторони один на одного.
Припустимо, що в основі призми лежить довільний n-кутник, сторони якого рівні ai. Індекс i пробігає значення від 1 до n. Площа одного прямокутника обчислюється так:
Si = ai*h.
Площа поверхні бічній Sb неважко обчислити, якщо скласти всі площі Si прямокутник. В такому випадку отримуємо кінцеву формулу для Sb прямий призми:
Sb = h*∑i=1n(ai) = h*Po.
Таким чином, щоб визначити площу бічної поверхні для прямої призми, необхідно помножити її висоту на периметр однієї основи.
Завдання з трикутною призмою

Припустимо, що задана пряма призма. Підстава - прямокутний трикутник. Катети цього трикутника дорівнюють 12 см і 8 см. Необхідно розрахувати обсяг фігури і її повну площу, якщо висота призми становить 15 см.
Для початку обчислимо обсяг прямої призми. Трикутник (прямокутний), що знаходиться в її підставах, має площу:
So = a1*a2/ 2 = 12 * 8/2 = 48 см2.
Як можна здогадатися, a1 і a2 у цій рівності є катетами. Знаючи площу основи і висоту (см. умова задачі) , можна скористатися формулою для V:
V = So* h = 48 * 15 = 720 см3.
Повна площа фігури утворена двома частинами: площами підстав і бічною поверхнею. Площі двох підстав рівні:
S2o = 2*So = 48 * 2 = 96 см2.
Для обчислення площі бічної поверхні необхідно знати периметр прямокутного трикутника. Обчислимо по теоремі Піфагора його гіпотенузу a3, маючи:
a3 = √(a12 + a22) = √(122 + 82) = 14,42 см.
Тоді периметр трикутника підстави прямої призми складе:
P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 см.
Застосовуючи формулу для Sb, яка була записана в попередньому пункті, отримуємо:
Sb = h*P = 15*34,42 = 516,3 см.
Склавши площі S2o і Sb, ми отримаємо повну площу поверхні досліджуваної геометричної фігури:
S = S2o + Sb = 96 + 516,3 = 612,3 см2.

Трикутна призма, яку виготовляють зі спеціальних видів скла, застосовується в оптиці при вивченні спектрів випромінюючих світло об`єктів. Такі призми здатні розкладати світло на складові частоти завдяки явищу дисперсії.
 Геометрична фігура призма. Властивості, види, формули обсягу і площі. Правильна трикутна призма
Геометрична фігура призма. Властивості, види, формули обсягу і площі. Правильна трикутна призма Що таке пряма призма? Формули довжин діагоналей, площі поверхні і обсягу фігури
Що таке пряма призма? Формули довжин діагоналей, площі поверхні і обсягу фігури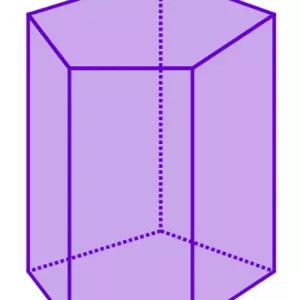 Площа поверхні прямої призми: формули і приклад задачі
Площа поверхні прямої призми: формули і приклад задачі Що таке призма? Види фігури. Формули для обсягу і площі. Призма у фізиці
Що таке призма? Види фігури. Формули для обсягу і площі. Призма у фізиці У чому вимірюється механічна робота? Формули для роботи газу і моменту сили. Приклад завдання
У чому вимірюється механічна робота? Формули для роботи газу і моменту сили. Приклад завдання Поняття про кутове прискорення. Формули кінематики і динаміки обертання. Приклад завдання
Поняття про кутове прискорення. Формули кінематики і динаміки обертання. Приклад завдання Формули для обчислення маси молекули, приклад задачі
Формули для обчислення маси молекули, приклад задачі Рівняння стану ідеального газу. Історичні передумови, формули і приклад завдання
Рівняння стану ідеального газу. Історичні передумови, формули і приклад завдання Одиниці вимірювання ньютон на метр і ньютон на метр квадратний. Приклад завдання
Одиниці вимірювання ньютон на метр і ньютон на метр квадратний. Приклад завдання